
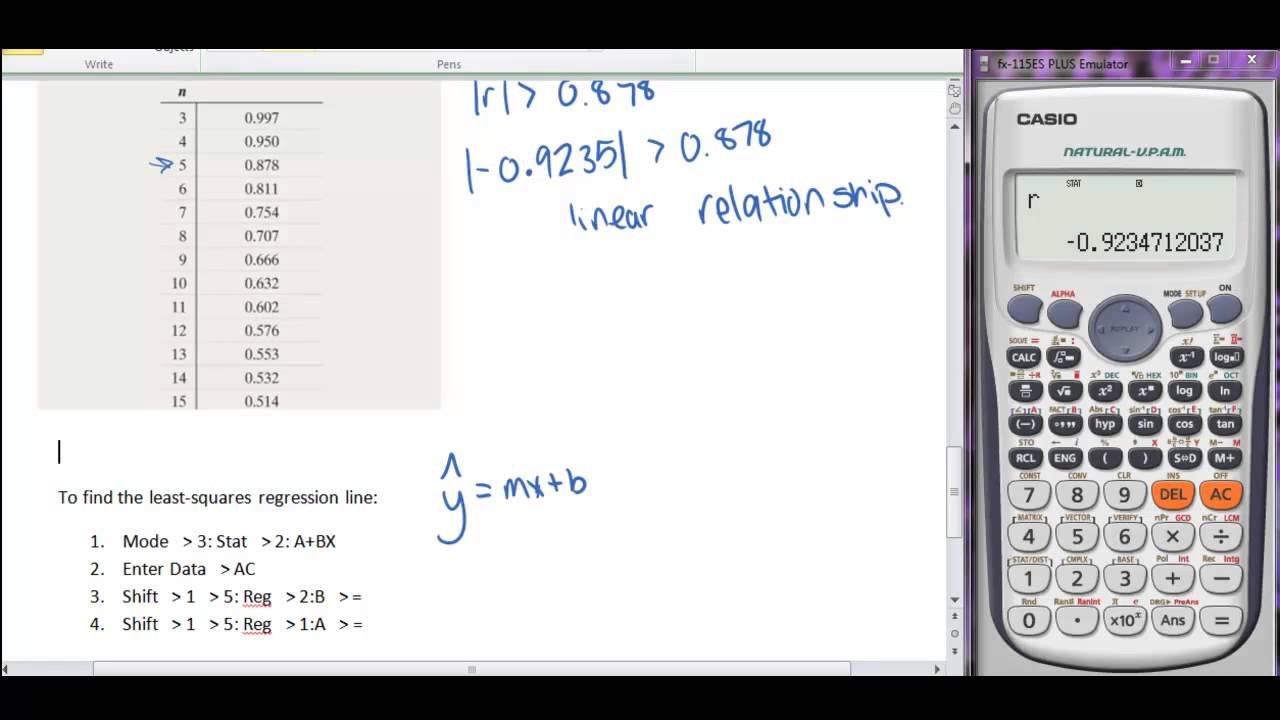
We then take each of the x values and minus x from each of them. The standard deviation for the y values, σ y, is 5. Now that we've gone through the steps for solving The only final step is to square this r value to get the N is the number of paired (x,y) data points.Īt to this point, we have solved for r, or the correlation We then divide this sum by the product of the standard deviations, σ x and σ y. We then take the sum of all of these products. The same for y values.Īfter this, for each (x,y) pair in the data set, we take each x value and minusįrom it we then multiply these values together. Subtracting the mean from each of the x values, squaring that result, adding up all the squares, dividing that number by the n-1 (where n is the number of items),Īnd then taking the square root of that result. The standard deviation for the x values is taken by

Σ x and the standard deviation for the y values is represented by σ y. The standard deviation for the x values is represented by The y values may be represent either by μ yīy taking the total for all the values and dividing itĪfter this, we have to calculate the standardĭeviations for the x and y values. The mean for the x values may be represented either by We're now going to go through all the stepsĬalculate the mean for the x values and the y values. So in order to solve for the r-squared value, weĭeviation of the x values and the y values. R-squared is really the correlation coefficient squared. Is essential for choosing the best-fitting regression line and, thus,Ĭan have the best machine-learning application. Thus, calculating the r-squared values for regression lines To predict future values based on the previous past data. Regression lines are obtained and these regression lines can be used And this regressionĪs you may be aware, regression lines are used a lot The regression line with an r-squared value of 0.92 is theīest-fitting regression line for the data points. So, say, we create 3 regression linesĪnd the r-squared values for each of them are 0.6, 0.85, and 0.92, To one is likely the best fit for the data set and probably be the You can then find the R-squared value for each Line is the best fit for a given data set.įor example, say that you created 3 regression lines for a data setīased on a variety of different methods. R-squared values are used to determine which regression The closer R is a value of 1, the better the fit the In essence, R-squared shows how good of a fit a regression R 2 is also referred to as the coefficient of Simple linear regression is a way to describe a relationship between two variables through an equation of a straight line, called line of best fit, that most closely models this relationship.This R-Squared Calculator is a measure of how close the data points of a data setĪre to the fitted regression line created.

If the calculations were successful, a scatter plot representing the data will be displayed.To clear the graph and enter a new data set, press "Reset".Press the "Submit Data" button to perform the computation.This flexibility in the input format should make it easier to paste data taken from other applications or from text books. Individual values within a line may be separated by commas, tabs or spaces. Individual x, y values on separate lines. X values in the first line and y values in the second line, or. x is the independent variable and y is the dependent variable. Enter the bivariate x, y data in the text box.This page allows you to compute the equation for the line of best fit from a set of bivariate data:


 0 kommentar(er)
0 kommentar(er)
